boj 7869 - 두 원

목차

개요

설명

코드

풀이 과정

개요

삼각함수를 이용해서 겹쳐진 두 원의 넓이를 구하는 문제입니다. 두 원이 존재할 수 있는 방법은 다음과 같이 세 가지 경우가 있습니다.

1) 두 원이 완전히 겹쳐지지 않은 경우

2) 일부가 겹친 경우

3) 한 원이 다른 원에 완전히 속한 경우

설명

먼저, 두 원의 원점 사이의 거리는 $d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$ 입니다.

1) 두 원이 완전히 겹쳐지지 않은 경우

두 원이 겹쳐지지 않기 위한 조건은 $d > r1 + r2$ 입니다. 이 때, 겹치는 넓이는 $0$ 입니다.

2) 일부가 겹친 경우

두 원이 일부만 겹치기 위한 조건은 $|r1 - r2| < d < r1 + r2$ 입니다.

이 때, 부채꼴을 이루는 각 $\alpha$와 $\beta$는 다음과 같습니다. 풀이 과정은 페이지 하단을 참고해주세요.

$$\alpha = 2cos^{-1} ((l^2 + r_1^2 - r_2^2) / (2lr_1)), \beta = 2cos^{-1} ((l^2 + r_2^2 - r_1^2) / (2lr_2))$$

다음 $r_1$ 입장에서 계산할 때, 노란색 색칠된 영역의 넓이를 구하고 2배를 하면 됩니다.

이 색칠된 부분의 넓이 $S_1$은 다음과 같습니다.

$$S_1 = ( r_1^2 \alpha - r_1^2 \alpha)/2$$

마찬가지로 반대 부분의 넓이 $S_2$도 다음과 같습니다.

$$S_2 = ( r_2^2 \beta - r_2^2 \beta)/2$$

따라서 정답은 다음과 같이 정리가 가능합니다.

$$Ans = S = S_1 + S_2 = r_1^2(\alpha - sin(\alpha)) + r_2^2(\beta - sin(\beta))$$

참고

각도가 $\theta$인 부채꼴의 넓이 = $r^2 \theta /2$,

두 변의 길이가 $a, b$이고, 그 변의 사이 각이 $\theta$인 삼각형의 넓이 = $ab \theta /2$

3) 한 원이 다른 원에 완전히 속한 경우

두 원점 사이의 거리 $d$가 $|r1 - r2|$ 보다 작아지면, 둘 중 반지름이 작은 원이 큰 원 내에 속해 있다는 의미입니다.

이 때, 겹치는 넓이는 $min(r1, r2)^2 * \pi$ 입니다.

코드

#include<stdio.h>
#include<math.h>

inline double pow(double a){
        return a*a;
}
inline double min(double a, double b){
        return a>b? b:a;
}
int main(){

        double x1,y1,r1, x2,y2,r2;
        scanf("%lf %lf %lf %lf %lf %lf",&x1, &y1, &r1, &x2, &y2, &r2);

        double l=sqrt(pow(x2-x1)+pow(y2-y1));
        double ANS = 0;
        if(r1+r2<=l){
                ANS = 0;
        }else if(r1+r2>l && abs(r1-r2)<l){
                double a = 2*acos((pow(l)+pow(r1)-pow(r2))/(2*l*r1));
                double b = 2*acos((pow(l)+pow(r2)-pow(r1))/(2*l*r2));
                ANS = pow(r1)*(a-sin(a))+pow(r2)*(b-sin(b));
                ANS /=2;
        }else{
                ANS = pow(min(r1,r2))*M_PI;
        }
        printf("%.3lf\n",ANS);
}

풀이과정

고교때 배운 cos 법칙과 삼각함수 합곱 공식은 거의 기억이 나지 않는 수준에 도달했습니다. 대신에 간단한 몇 가지 사실을 이용해서 계산하면 식을 유도할 수 있습니다.

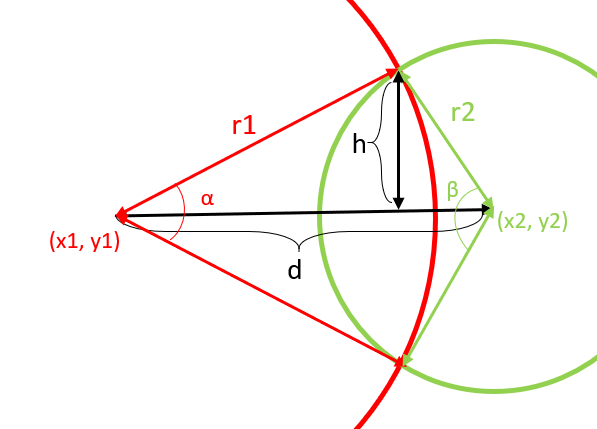
이 교차점에서 $d$는 우리가 이미 계산해서 알 수 있습니다. ( $d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$ )

1) 높이 h를 이용

높이 $h$를 이용하면 다음과 같은 식을 유도할 수 있습니다.

$$\begin{align} h = r_1 sin(\alpha /2) = r_2 sin(\beta / 2) \tag{1} \ \end{align}$$

2) d의 표현식

두 원점 사이의 거리 $d$는 각 원의 반지름에 cos하여 더한 값과 같습니다.

$$\begin{align} d = r_1 cos(\alpha/2) + r_2 cos(\beta/2) \tag{2} \ \end{align}$$

3) 연립

식 $(1)$에서 $sin^2(\alpha) + cos^2(\alpha) = 1$ 임을 이용하면 다음과 같이 변경할 수 있습니다.

$$\begin{align} h^2 = r_1^2\ sin^2(\alpha/2) &= r_2^2\ sin^2(\beta/2) \tag{3}\\ r_1^2 (1-cos^2(\alpha/2)) &= r_2^2 (1-cos^2(\beta/2)) \tag{4}\\ r_1^2 -r_1^2\ cos^2(\alpha/2) &= r_2^2 - r_2^2\ cos^2(\beta/2) \tag{5}\\ \end{align}$$

 

식 $(5)$를 정리하면 다음 식을 얻을 수 있습니다.

 

$$\begin{align} r_1^2\ cos^2(\alpha/2) = r_1^2 - r_2^2 + r_2^2\ cos^2(\beta/2) \tag{6}\\ \end{align}$$

 

식 $(2)$에서 우선 계산의 편의를 위해 $d$를 제곱해줍니다.

$$\begin{align} d^2 &= r_1^2\ cos^2(\alpha/2) + r_2^2\ cos^2(\beta/2) + 2r_1r_2\ cos(\alpha/2)\ cos(\beta/2) \tag{7} \end{align}$$

 

여기서 식 $(6)$을 대입하면

$$\begin{align} d^2 &= r_1^2 - r_2^2 + 2r_2^2\ cos^2(\beta/2) + 2r_1r_2\ cos(\alpha/2)\ cos(\beta/2) \tag{8} \\ d^2 -r_1^2 + r_2^2 &=2r_2^2\ cos^2(\beta/2) + 2r_1r_2\ cos(\alpha/2)\ cos(\beta/2) \tag{9} \\ (d^2 -r_1^2 + r_2^2)/2r_2 &=r_2\ cos^2(\beta/2) + r_1\ cos(\alpha/2)\ cos(\beta/2) \tag{10} \\ &=cos(\beta/2)(r_2\ cos(\beta/2) + r_1\ cos(\alpha/2) ) \tag{11} \\ \end{align}$$

 

식 $(11)$에서 기존의 식 $(2)$를 대입하면

$$\begin{align} (d^2 -r_1^2 + r_2^2)/2r_2 &=cos(\beta/2)(d) \tag{12} \\ (d^2 -r_1^2 + r_2^2)/2dr_2 &= cos(\beta/2) \tag{13} \\ \end{align}$$

 

이제 마지막 식에서 cos 역함수를 취해주면 다음과 같은 결과를 얻어낼 수 있습니다.

$$\begin{align} \beta &= 2cos^{-1} ((d^2 -r_1^2 + r_2^2)/2dr_2) \tag{14} \\ \end{align}$$

$\alpha$에 대해서도 반대로 똑같이 취해주면 됩니다.