- Today
- Total
Byeo
boj 1069 - 집으로 본문
목차
개요
이 문제는 2차원 좌표계에서 어느 직선상의 출발점에서 도착점까지 걸어서 혹은 점프로 가장 빠르게 도착하는 방법을 찾는 문제입니다.
가장 주의해야 할 점은 2차원 상에서 아무렇게 움직일 수 있다는 점입니다. 따라서 점프가 직선상에서만 국한된 것이 아닌, 직선에서 외부로 잠시 나갔다가 다시 도착점으로 점프하는게 최소 비용일 수 있습니다.
그래서 이 문제는 다음과 같이 케이스를 나눠서 풀면 됩니다.
1) 전부 걸어서 가는 경우
2) 처음부터 끝까지 점프해서 도착점에 딱 도착하는 경우
3) 도착점에서 가장 가까운 지점까지 점프한 뒤, 남은 거리는 걸어서 가는 경우
4) 도착점을 넘어서까지 점프를 한 뒤, 남은 거리는 걸어서 가는 경우
위 4가지를 모두 고려해서 계산한 뒤, 최솟값을 구하면 최소비용입니다.
단순히 각 경우의 비용을 보고 싶으시다면 요약으로 이동해주세요.
설명
각 케이스를 그림으로 한 번 살펴볼까요?
인풋은 $x, y, d, t$ 입니다.
먼저 출발점과 도착점 사이의 거리를 $l= \sqrt{x^2+y^2}$ 이라고 하겠습니다.
1) 전부 걸어서 가는 경우
말 그대로 걸어서 가는 경우입니다. D<T일 때 뿐만 아니라, jump 거리 단위가 클때도 전부 걸어서 가는 경우가 유리할 수 있습니다.

이 경우 비용은 그저 걸어갔으므로 $l$ 입니다.
2) 처음부터 끝까지 점프해서 도착점에 딱 도착하는 경우
처음 접했을 때, 이 경우가 항상 존재하는지를 가늠하기 어려웠습니다. 그러나 점프를 쉽게 원으로 생각해보면 이해하기 쉽습니다.

source에서 한 번 점프하면 1번 원 어디로든 갈 수 있습니다.
마찬가지로 두 번 점프하면 2번 원 어디로든 갈 수 있습니다.
세 번 점프하면 3번 원 위의 점, 네 번 점프하면 4번 위의 점 어디로든 위치할 수 있게되지요.
그러면, 점프만으로 destination에 도달할 수 있음을 항상 보장할 수 있을까요? 이는 destination에서 원 하나만 그려보면 이해가 가실겁니다.
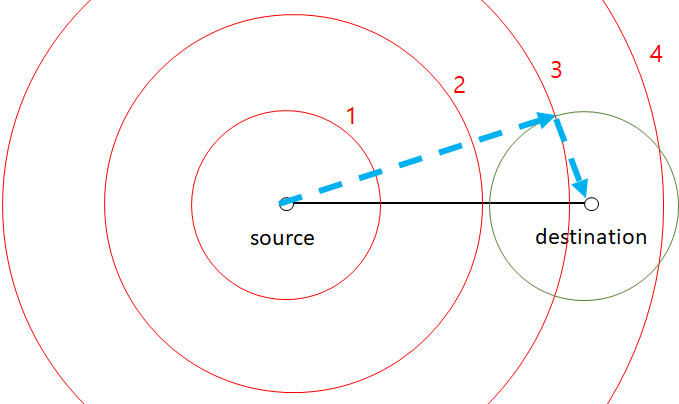
이 그림에서 점프만으로 도착점에 가는 방법은 하늘색 점선을 따라가면 됩니다. source에서 동심원을 계속 그려나가면 destination에서 점프 한 번으로 갈 수 있는 위치를 원으로 그릴 때 반드시 교점이 생길 수 밖에 없습니다. 점프 거리는 일정하므로 반지름이 같기 때문이죠.
이 그림에서 이동 비용은 점프 4번 ($4t)$ 입니다. destination이 3번 원과 4번 원 사이에 위치하므로 4번 점프해서 도달 할 수 있는 것이죠. 즉, $N$번과 $N+1$번 사이에 destination이 존재하는 경우, 비용은 $(N+1)t$ 입니다.
주의해야 할 점은, 이 방법으로 source에서 destination으로 갈 때는 최소 2번의 점프를 필요로 합니다.
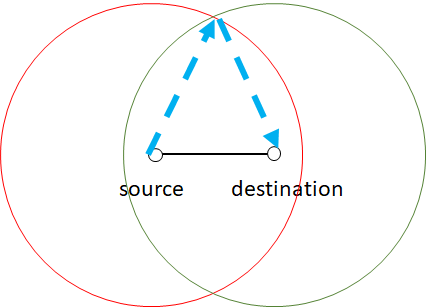
destination이 1번 원보다 안쪽에 있어도 비용은 $(0+1)t$ 가 아닌 $2t$입니다.
3) 도착점에서 가장 가까운 지점까지 점프한 뒤, 남은 거리는 걸어서 가는 경우

이 경우는 위 그림처럼 하늘색 점선을 따라 점프한 뒤 남은 주황색 거리만큼 걸어가는 방법입니다.
비용은 destination이 원 $N$과 원 $N+1$ 사이에 위치할 경우, $tN+(l-dN)$ 입니다.
4) 도착점을 넘어서까지 점프를 한 뒤, 남은 거리는 걸어서 가는 경우
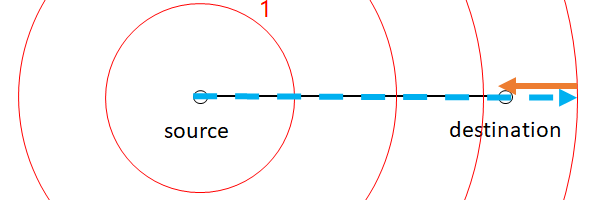
이 경우는 위 그림처럼 하늘색 점선을 따라 destination을 넘어서까지 점프를 한 뒤, 걸어서 되돌아 오는 경우입니다.
비용은 destination이 원 $N$과 원 $N+1$ 사이에 위치할 경우, $t(N+1)+(d(N+1)-l)$ 입니다.
그러나 이 경우는 "2) 점프로만 도달하는 경우" 보다 항상 큽니다.
$t(N+1)+(dN+d-l) > t(N+1)$
그러면 언제 의미가 있느냐. source에서 destination까지의 거리가 jump 거리보다 짧을 때 이 케이스를 고려하게 됩니다.

즉, 위 그림과 같은 경우에는 $2t$과 $t+(d-l)$ 사이에서 저울질 해야하는 것이죠.
요약
각 경우의 비용은 아래와 같습니다.
1) 전부 걸어서 가는 경우: $l$
2) 처음부터 끝까지 점프해서 도착점에 딱 도착하는 경우: $max(\ (N+1)t, \ 2t)$
3) 도착점에서 가장 가까운 지점까지 점프한 뒤, 남은 거리는 걸어서 가는 경우: $tN+(l-dN)$
4) 도착점을 넘어서까지 점프를 한 뒤, 남은 거리는 걸어서 가는 경우: $t(N+1)+(d(N+1)-l)$
위 4가지 경우에서 최소값을 구해 출력하면 되겠습니다.
코드
점프 횟수 $N$은 while문을 통해서 구할 수 있습니다.
#include<stdio.h>
#include<math.h>
double min(double a, double b){
return a > b? b : a;
}
int max(int a, int b){
return a > b? a : b;
}
int main(){
int x,y,d,t;
scanf("%d %d %d %d",&x, &y, &d, &t);
double l = sqrt(x*x+y*y);
double type1 = l;
double type2 = 0;
double type3 = 0;
double type4 = 0;
int N = 0, jumpD = 0;
while(jumpD <= l){
jumpD += d;
N += 1;
}
N-=1; jumpD-=d;
type2 = max(t*(N+1), 2*t);
type3 = t*N+(l-d*N);
type4 = t*(N+1)+(d*(N+1)-l);
//printf("%lf %lf %lf %lf\n",type1, type2, type3, type4);
printf("%.16lf\n", min(min(type1, type2), min(type3,type4)));
}'알고리즘 (Algorihtm) > 백준' 카테고리의 다른 글
| boj 7869 - 두 원 (0) | 2021.12.30 |
|---|---|
| boj 7626 - 직사각형 (2) | 2021.12.29 |
| boj 17131 - 여우가 정보섬에 올라온 이유 (0) | 2021.07.27 |
| boj 5419 - 북서풍 (0) | 2021.07.25 |
| boj 2836 - 수상 택시 (0) | 2021.07.21 |




