- Today
- Total
Byeo
boj 7626 - 직사각형 본문
목차
개요
이 문제는 Segment Tree 자료구조와 Sweeping 알고리즘을 함께 활용하여 풀어야 하는 문제입니다. 추가로 좌표의 범위가 상당히 넓기 때문에 (0 ~ 1,000,000,000) 좌표 압축까지 병행해야 합니다.
문제의 Key Idea는 Segment Tree에 어떤 정보를 저장할 것이냐 입니다. 예를 들어, x축으로 Sweeping을 진행한다고 할 때, 직사각형의 넓이를 구하기 위해서는 각 x좌표 별로 직사각형에 포함되는 y영역과 그렇지 않은 영역을 구분해야 합니다.
이를 구분하기 위해서 기존 방식의 Segment Tree보다는 구간 Update query를 통해 현재 활성화 된 직사각형의 개수가 몇 개인지 구간 별로 관리하고, 넓이를 단번에 파악할 수 있도록 전체 직사각형 y의 부분 합을 저장하는 변형된 방식을 사용해야 합니다.
요약
1) y좌표를 기준으로 좌표 압축을 실행한다.
2) x좌표를 정렬해서 오름차순으로 sweep을 실행한다.
모든 직사각형을 탐색할 때 까지 3, 4, 5를 반복
3) x좌표 차이 (너비)와 Segment Tree의 root node에 저장된 높이 합을 곱해서 정답에 추가한다.
4) 직사각형이 시작하는 경우, Segment Tree에 구간 update query를 실행해서 count++ 와 자신의 직사각형의 높이를 기록한다.
5) 직사각형이 끝나는 경우, Segment Tree에 구간 update query를 실행해서 count--를 한다. count가 0인 경우, child node의 부분합으로 높이를 변경한다. (Leaf node일 경우, 0으로 기록한다)
설명
다음과 같이 6개의 직사각형 넓이 합을 알고 싶다고 해봅시다. (정답: 7080)
6
30 60 10 124
130 140 44 50
100 110 3 124
10 50 3 44
40 110 16 50
80 90 3 10위를 그림으로 나타내면 다음과 같습니다.

여기서 y좌표의 범위가 0부터 10억까지 가능합니다. Segment Tree의 node를 10억 개 만들 수 없으므로 좌표 압축을 하는 것이 좋겠죠. 유의미한 좌표인 3을 0번으로 기준 삼아 124까지 좌표를 압축하면 아래와 같이 나타낼 수 있습니다.

그리고 계산을 통해서 좌표가 압축된 y좌표 사이의 실제 길이도 알 수 있죠. (그림의 우측)
그러면 이제 X축의 왼쪽부터 오른쪽으로 차례대로 Sweep하면서 활성화 된 y축의 길이를 Segment Tree에 저장하면 됩니다.
Step 1) x = 10
x좌표가 10일 때를 살펴보면, 직사각형이 시작되고 있습니다. 그렇다면 y좌표 0이상 3미만이 활성화 된 구간이므로 Segment Tree에 저장하고, 차례로 node들을 수정해줍니다.

만약 Segment Tree가 오른쪽과 같이 구성되어 있다고 가정합시다. 각 node들은 Y축 실제 길이 / 선분 활성화 개수를 저장합니다.
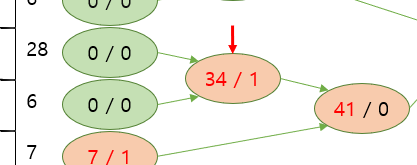
이 상태에서 node들을 수정해가던 중에 1이상 3미만은 leaf node까지 가지 않고, 한꺼번에 표현이 가능한 node가 존재합니다. 이 경우에는 해당 node를 직접 수정하고 child node들은 수정하지 않습니다. Leaf까지 직접 수정해서 전체를 수정하는 방법도 있겠지만, 이 방법이 더 효율적이겠죠?
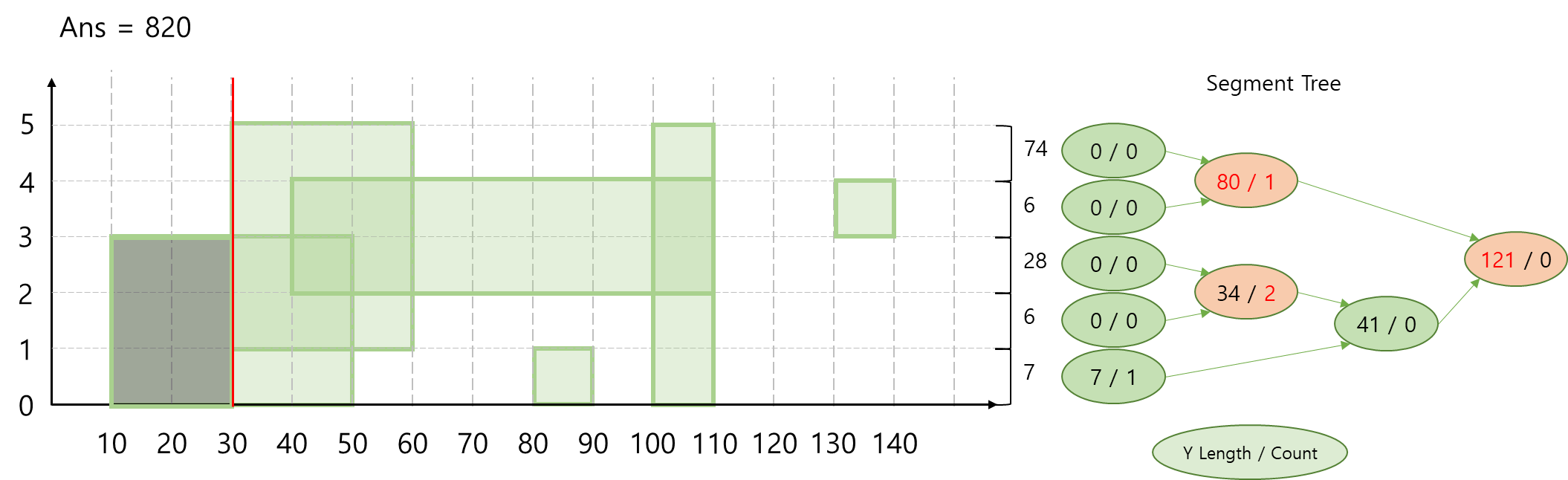
Step 2) x = 30
다음 y축 활성이 변화하는 지점은 x가 30일 때입니다. 이 때, 현재까지 활성화 된 y축 길이의 합 (Segment Tree의 root node)과 x좌표 차이를 곱해서 정답에 더해줍니다.

위에서 검은색으로 칠해진 영역은 계산이 끝난 직사각형입니다.
이제, 새로운 직사각형 1이상 5미만이 등장합니다. 마찬가지로 해당 부분에 맞는 node들을 수정해줍니다.
Step 3) x = 40
다음으로 y축 활성이 변하는 좌표는 x가 40일 때입니다. 마찬가지로 현재까지 활성화 된 y좌표의 길이의 합과 x좌표 차이를 곱해줍니다.

위 그림에서 알 수 있듯이, 2이상 3미만과 3이상 4미만은 각각 다른 sub node들이 담당을 하고 있습니다. 따라서 leaf node까지 탐색하여 수정을 해줘야 합니다.
그러나, 이 leaf node들을 수정을 해주더라도 이미 parent node가 활성화 되어 있기 때문에, 재귀적으로 수정해야 할 필요는 없습니다. (즉, 이전 직사각형에 포함되는 영역입니다.)
Step 4) x = 50
처음으로 만났던 직사각형이 끝나는 좌표입니다. 먼저, 정답 값을 앞서 했던 방법과 같은 방식으로 update 해줍니다.
앞서 직사각형을 만났던 때를 생각해봅시다. count에 +1을 해주던 방식처럼 구간 업데이트를 통해 count를 1 감소 시킵니다.

특히, 0이상 1미만 구간의 경우에는 count가 0으로 변했으므로 재귀적으로 parent들을 update 해줘야 합니다.
Step 5) x = 60
x좌표가 60일 때는 다음과 같이 수정됩니다.

Leaf node가 아니라 subnode의 count가 0이된 경우, Y 길이의 부분합 값은 child들의 합으로 변경해줘야 합니다.
Step 6) x = 80
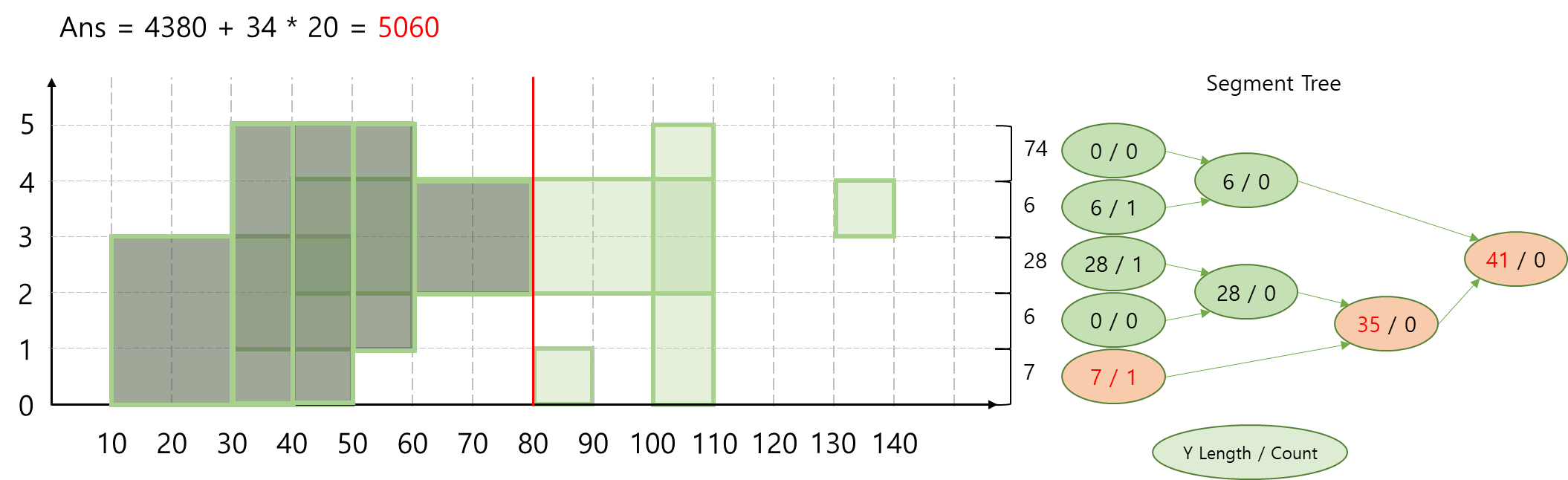
0이상 1 미만의 직사각형이 시작되었으므로 Segment Tree에 반영해줍니다.
Step 7) x = 90

Step 8) x = 100
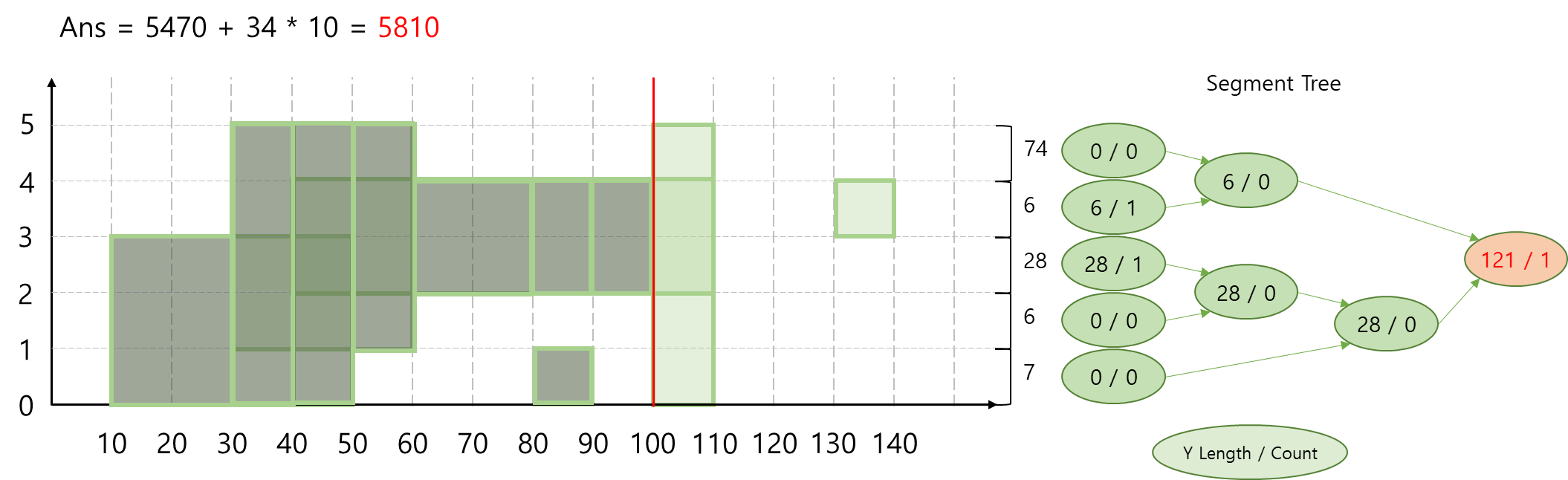
모든 y좌표가 활성화 됩니다. 따라서 root node만 수정해주면 됩니다.
Step 9) x = 110
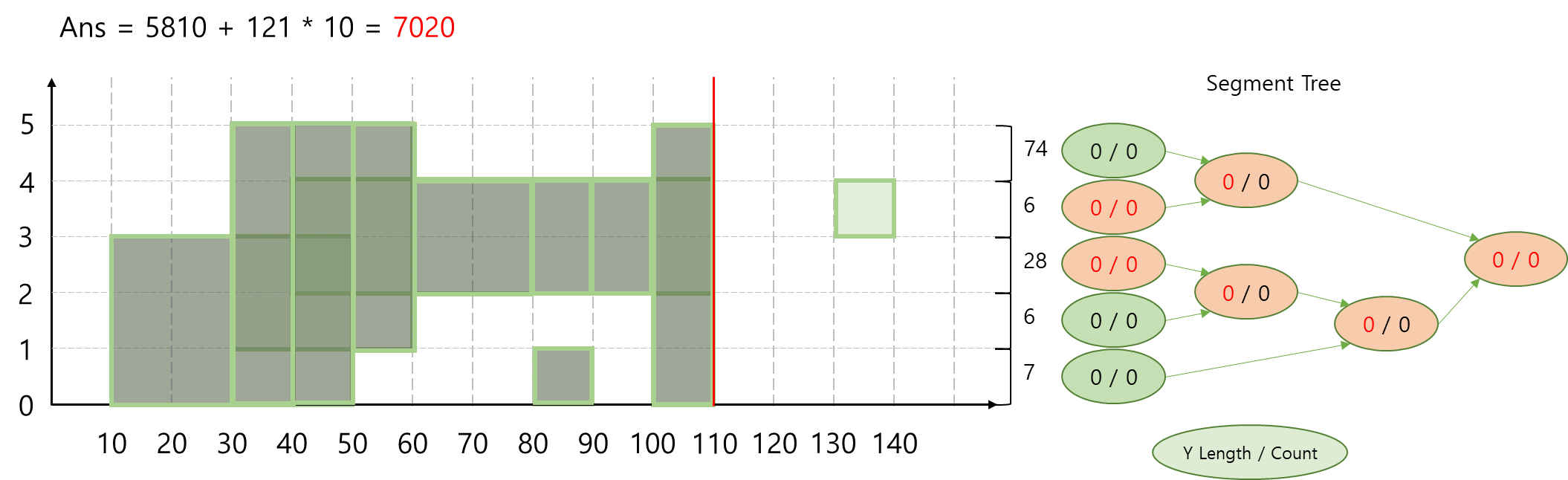
동시에 두 직사각형이 종료됩니다. 차례차례 순서 상관 없이 모두 비활성화 해주면 됩니다.
Step 10) x = 130, x = 140
마찬가지로 x좌표가 130일 때 있는 작은 직사각형도 같은 방법으로 해주면 됩니다. 정답은 7020 + 10 * 6
7080이 되겠네요.
코드
#include<stdio.h>
#include<algorithm>
using namespace std;
int N;
class Point{
public:
int val;
int idx;
int y1;
int y2;
bool operator<(Point a) const{
return this->val < a.val;
}
};
class Y{
public:
int val;
int idx;
bool operator<(Y a) const{
return this->val < a.val;
}
};
Point x[400002];
Y y[400002];
long long int cnt[1600000];
long long int sum[1600000];
class Tree{
public:
Tree(){
for(int i=0;i<N*8;i++){
cnt[i] = 0;
sum[i] = 0;
}
}
void update(int left, int right, int start, int end, int k, int val){
int mid = (start+end)/2;
int ret = 0;
if(start >=left && end <= right){
cnt[k] += val;
}else{
if(left<=mid) update(left, right, start, mid, k*2, val);
if(right>mid) update(left, right, mid+1, end, k*2+1, val);
}
if(cnt[k]){
sum[k] = y[end+1].val - y[start].val;
}else{
if(start==end) sum[k] = 0;
else sum[k] = sum[k*2] + sum[k*2+1];
}
}
};
int main(){
long long int ANS = 0;
scanf("%d",&N);
for(int i=0; i<N;i++){
int a = 2*i, b = 2*i+1;
scanf("%d %d %d %d",&x[a].val, &x[b].val, &y[a].val, &y[b].val);
x[a].idx = y[a].idx = a;
x[b].idx = y[b].idx = b;
}
sort(y,y+2*N);
//Coordinate compression
for(int i=0;i<2*N;i++){
int arr_idx = y[i].idx / 2;
if(y[i].idx %2==0){
x[arr_idx*2].y1 = i;
x[arr_idx*2+1].y1 = i;
}else{
x[arr_idx*2].y2 = i;
x[arr_idx*2+1].y2 = i;
}
}
sort(x,x+2*N);
for(int i=0;i<2*N;i++){
}
Tree *t = new Tree();
for(int i=0;i<2*N;i++){
if(i>0){
ANS += sum[1] * (x[i].val - x[i-1].val);
}
if(x[i].idx % 2 ==0){ //Rectangle start
t->update(x[i].y1, x[i].y2-1, 0, 2*N-1,1, 1);
}else{//Rectangle end
t->update(x[i].y1, x[i].y2-1, 0, 2*N-1,1, -1);
}
}
printf("%lld\n",ANS);
return 0;
}'알고리즘 (Algorihtm) > 백준' 카테고리의 다른 글
| boj 17435 - 합성함수와 쿼리 (0) | 2023.12.25 |
|---|---|
| boj 7869 - 두 원 (0) | 2021.12.30 |
| boj 1069 - 집으로 (0) | 2021.08.06 |
| boj 17131 - 여우가 정보섬에 올라온 이유 (0) | 2021.07.27 |
| boj 5419 - 북서풍 (0) | 2021.07.25 |




