- Today
- Total
Byeo
최소신장트리 (Minimum Spanning Tree) - 크루스칼 알고리즘 본문
1. 설명
MST를 구하는 유명한 알고리즘의 두 번째로는 크루스칼 알고리즘은 greedy 알고리즘으로 볼 수 있다. 간선의 가중치가 작은 것부터 하나하나 MST에 포함시켜보면서 cycle이 생기는 지 매번 판단하는 방법으로 이뤄진다.
이전 포스트의 프림 알고리즘 예제에서 사용했던 예제를 그대로 사용해보자!
추가로 MST가 무엇인지 알고 싶다면: 링크
2. 예제
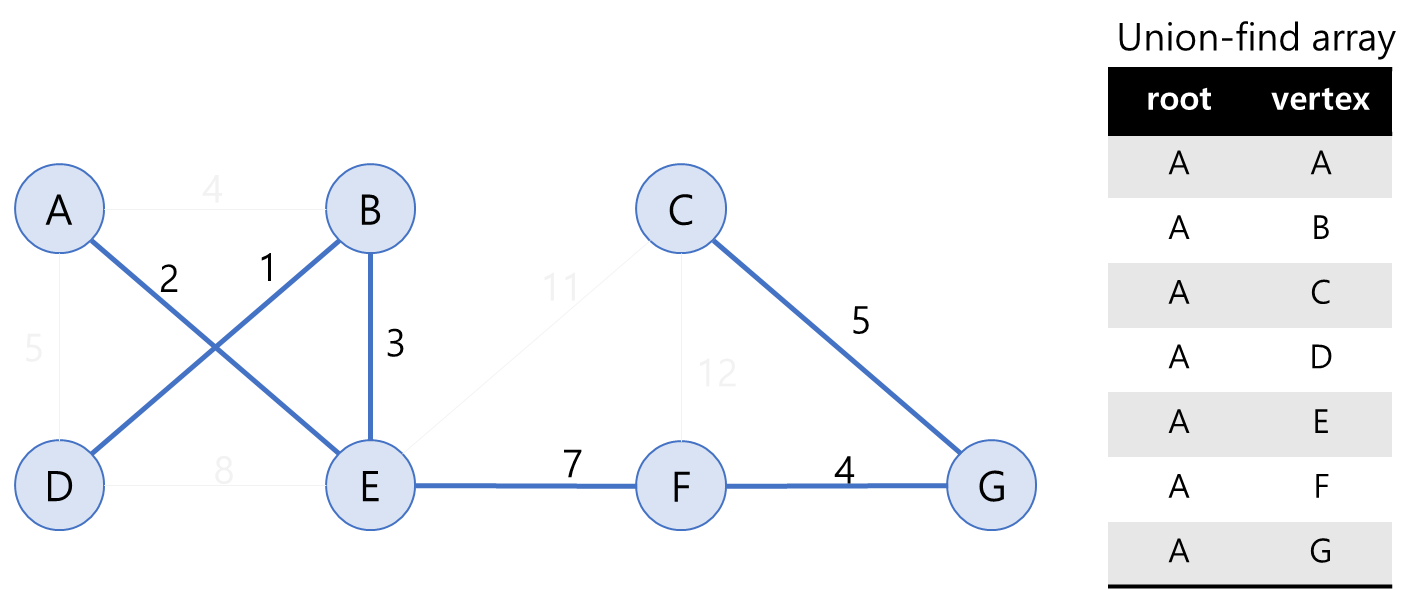
(1) 초기 환경이 다음과 같다고 하자.

크루스칼 알고리즘은 가중치가 작은 간선부터 차례로 MST에 포함시켜 보는 것이다. 만약 포함시켰는데 MST에 위배된다면 뺀다.
오른쪽은 union-find array를 나타낸다. 자세히는, 각 vertex가 속해있는 그룹의 주인 (root, 특별한 역할이 있는 노드는 아니다. 단순히 학창 시절 '주번' 같은 친구)이 누구인지를 관리하는 표이다. 처음에는 어느 누구도 동일한 그룹을 형성하고 있지는 않다.
가장 작은 간선은 BD로 그 가중치는 1이다. 그리고 B와 D의 root는 각각 B와 D로 다른 그룹에 속해있다.
(2) 간선 BD 선택.

B와 D는 이제 하나의 그룹으로 묶였다. 따라서 D의 root를 B로 설정해준다. (B의 root를 D로 설정해도 무방하다. 이 포스트에서는 일관되게 앞선 알파벳으로 설정한다고 하자.)
다음은 간선 AE가 2로 남은 것중에 가장 작다. A의 root와 E의 root는 각각 A와 E로 다른 그룹에 속해있다. 따라서 MST에 추가가 가능하다.
(3) 간선 AE 선택.

마찬가지로 E의 root를 A로 바꿔준다.
다음은 가중치 3의 간선 BE이다. B의 root는 B, E의 root는 A이므로 서로 다른 그룹에 속해있다. 따라서 MST에 속할 수 있다.
(4) 간선 BE 선택.
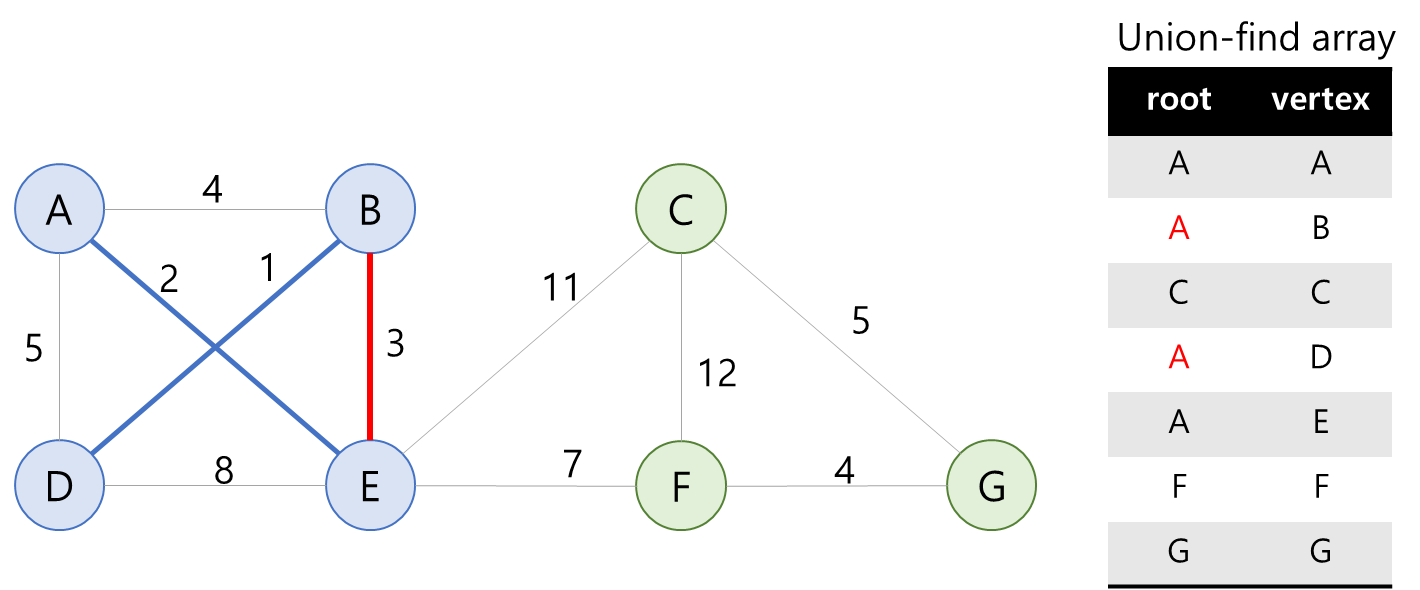
여기서는 B에 속해있던 모든 그룹의 root를 A로 바꿔줘야 한다. B와 D가 속해있었으므로, B와 D의 root를 A로 바꿔주자.
다음으로는 가중치가 4인 간선으로 간선 AB와 간선 FG가 있다.
간선 AB: A의 root와 B의 root는 둘 다 A로, 같은 그룹에 속해있다. 이 간선을 MST에 추가하는 순간 cycle이 생기게 된다. 따라서 스킵!
간선 FG: F의 root는 F, G의 root는 G로 다른 그룹에 속해있다. 따라서 MST에 추가가 가능하다.
(5) 간선 FG 선택
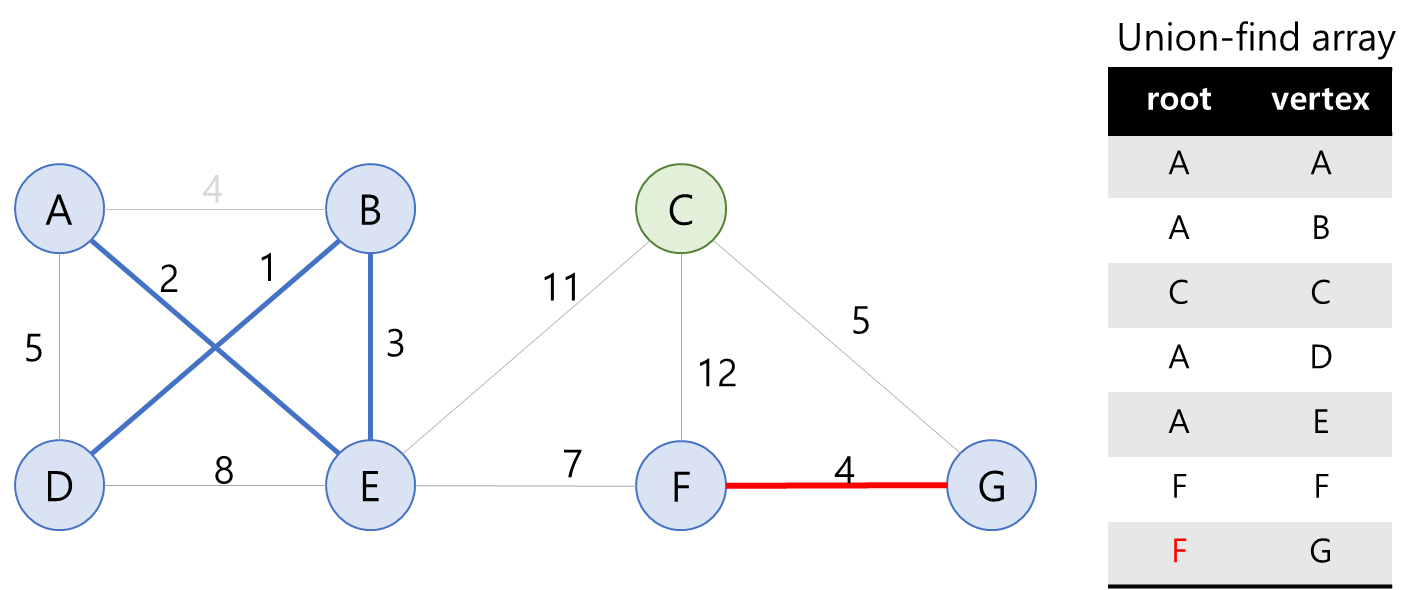
G의 root를 F로 변경해준다. 이제 둘은 같은 그룹이 되었다. 주의할 점은 ABDE와 FG는 다른 그룹이다! ( ABDE / C / FG)
다음 간선은 가중치가 5다.
간선 AD: 이제 이 즈음이면 익숙해졌을 것이다~ A의 root는 A, D의 root는 A로 동일한 그룹에 속해있다.
간선 CG: C의 root는 C, G의 root는 F로 다른 그룹에 속해있다. 따라서 MST에 추가가 가능하다.
(6) 간선 CG 선택
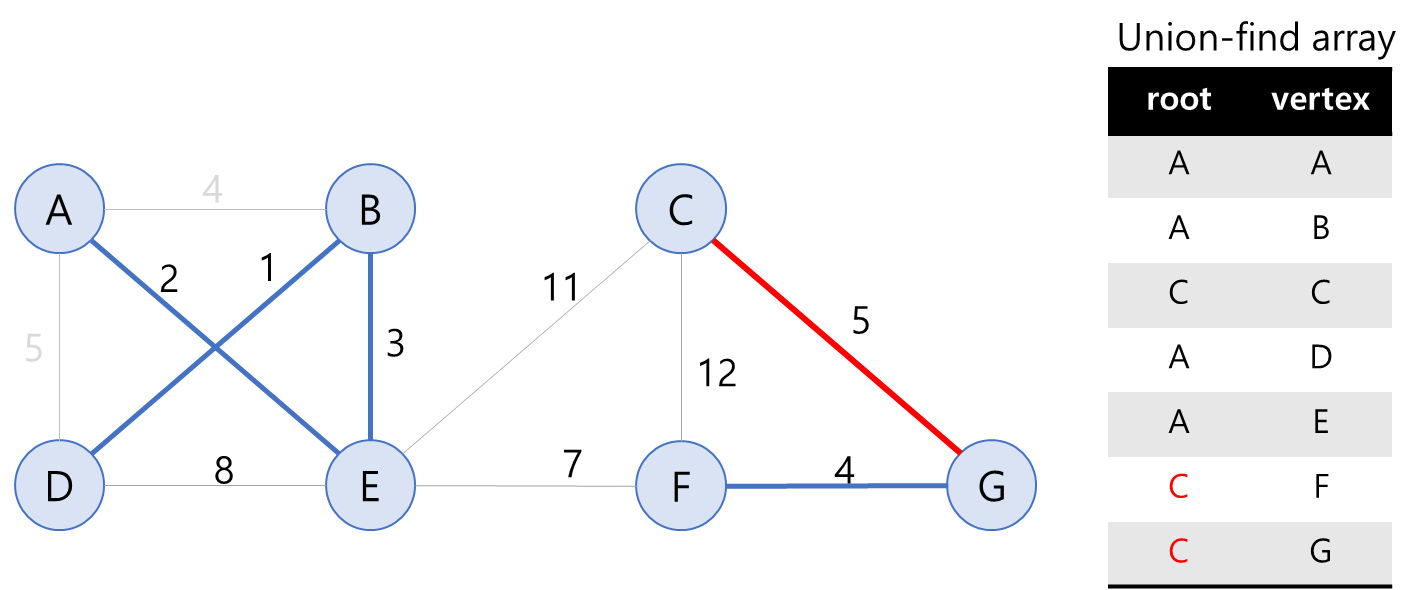
그룹 C와 그룹 FG를 합침을 의미하기 위해서, F와 G의 root를 C로 설정해준다.
다음 작은 간선은 7로 간선 EF가 해당한다. E의 root는 A, F의 root는 C로 다른 그룹에 속해있어 MST에 추가가 가능하다.
(7) 간선 EF 선택
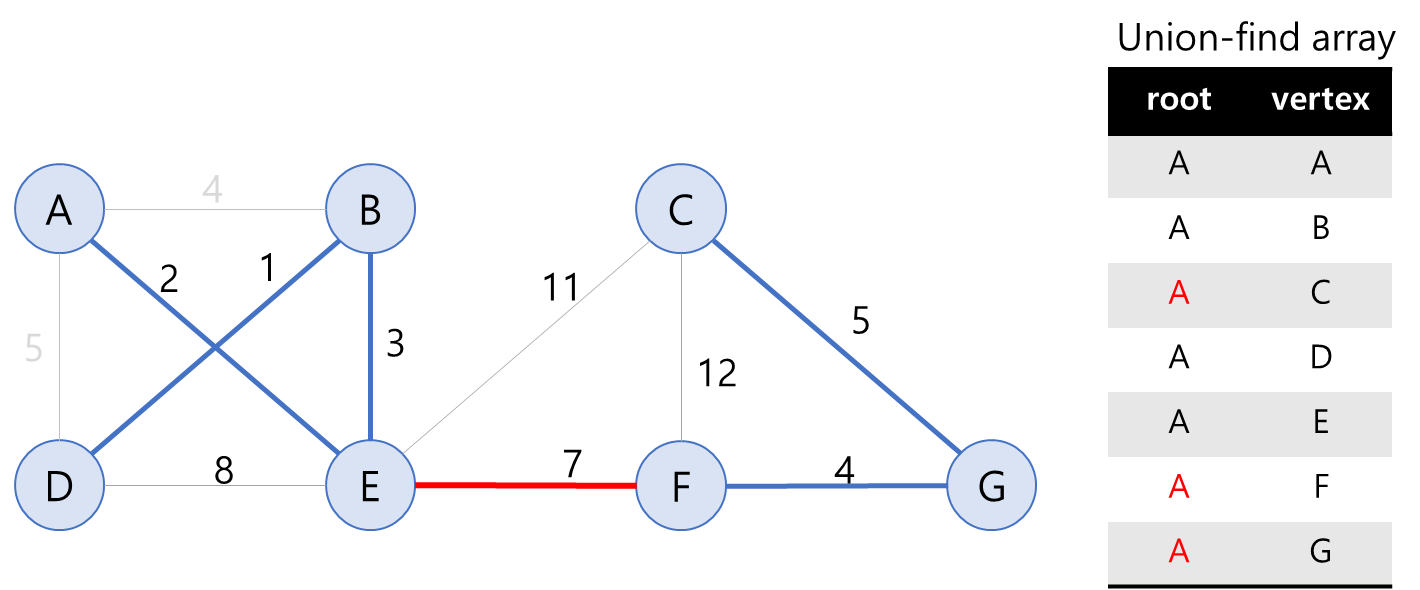
ABDE와 CFG가 같은 그룹임을 의미하도록 하기 위해서, CFG의 각 root를 A로 변경해준다.
간선 EF를 추가하면서 모든 노드가 동일한 그룹에 속해있게 되었다. 이 시점에서 MST 구성이 완성된다.
간선 DE, 간선 CE, 간선 CF는 검사를 하지 않은 노드이다. 따라서 검사 절차는 걸쳐야 하나, 결국에 모두가 동일한 그룹에 속해있어 MST에 추가되지 않는다. 따라서 이 과정은 스킵!
(8) 완성
시간복잡도
간선 가중치를 가장 작은 것부터 오름차순으로 정렬하면 된다. O(ElogE)
Union-find (disjoint-set) algorithm의 경우에는 O((V+E)α(V))로, α는 인버스 애커만 함수로서 굉장히 느리게 상승하는 값이다. O(α(V))=O(logV)=O(logE)로 볼 수 있고, 이는 결국 정렬시간에 한참 못미쳐 최종적으로 O(ElogE)가 된다. [Union-find 알고리즘 출처: CLRS]
Union-find의 시간복잡도는 구현에 따라 변종이 많은 값으로 확인된다.: [위키피디아] 다만 아래 코드에 작성된 예제는 path compression만 적용되어있어 약간의 윗 문단에서 설명했던 union-find 시간복잡도는 살짝 증가할 것으로 보인다.
3. 코드
C++
#include<stdio.h>
#include<vector>
#include<algorithm>
using namespace std;
int find_root(int parent[], int a){
if(parent[a] == a){
return a;
}else{
return parent[a] = find_root(parent, parent[a]);
}
}
void make_union(int parent[], int a, int b){
parent[b] = a;
}
bool cmp(int *a, int *b){
return a[2] < b[2];
}
int main(){
int v, e;
scanf("%d %d",&v,&e);
vector<int*> edges;
// Input
for(int i = 0; i < e; i++){
int a,b,c;
scanf("%d %d %d", &a, &b, &c);
edges.push_back(new int[3]{a, b, c});
}
// KRUSKAL
sort(edges.begin(), edges.end(), cmp);
int parent[10001];
int ANS = 0;
for(int i=1 ; i < v+1; i++){
parent[i] = i;
}
for(auto itr : edges){
int a_root = find_root(parent, itr[0]);
int b_root = find_root(parent, itr[1]);
if(a_root != b_root){
make_union(parent, a_root, b_root);
ANS += itr[2];
}
}
printf("%d\n", ANS);
}RUST
use std::io::{stdin, Read};
use std::cmp::Ordering;
fn find_root(mut parent: &mut [usize; 10001], a: usize) -> usize{
if parent[a] == a{
a
}else{
parent[a] = find_root(parent, parent[a]);
parent[a]
}
}
fn make_union(mut parent: &mut [usize; 10001], a: usize, b: usize){
parent[b] = a;
}
fn main() {
let mut input = String::new();
stdin().read_to_string(&mut input).unwrap();
let mut input = input.split_ascii_whitespace().flat_map(str::parse::<i32>);
let v = input.next().unwrap() as usize;
let e = input.next().unwrap() as usize;
let mut edges : Vec<(usize, usize, i32)> = vec![];
// Input
for _i in 0..e{
let a = input.next().unwrap() as usize;
let b = input.next().unwrap() as usize;
let c = input.next().unwrap();
edges.push((a, b, c));
}
// KRUSKAL
edges.sort_by(|a, b| a.2.cmp(&b.2));
let mut parent: [usize; 10001] = [0; 10001];
let mut ANS = 0;
for _i in 1..(v+1){
parent[_i] = _i;
}
for edge in &edges{
let a_root = find_root(&mut parent, edge.0);
let b_root = find_root(&mut parent, edge.1);
if a_root != b_root {
make_union(&mut parent, a_root, b_root);
ANS += edge.2;
}
}
println!("{ANS}");
}'알고리즘 (Algorihtm) > 공통' 카테고리의 다른 글
| 이분 매칭 (Bipartite Matching) 알고리즘 (0) | 2024.01.14 |
|---|---|
| 최소신장트리 (Minimum Spanning Tree) - 프림 알고리즘 (0) | 2023.10.29 |
| VScode 설치, 원격 서버 접속 (0) | 2023.10.15 |
| 스위핑 (Sweeping) (0) | 2021.07.20 |
| 세그먼트 트리 (Segment Tree) (0) | 2021.07.02 |




