- Today
- Total
Byeo
이분 매칭 (Bipartite Matching) 알고리즘 본문
문과 감성
이분 매칭 알고리즘은 사랑과 전쟁 이다.
- 관심 있는 이성이 솔로라면 바로 커플을 맺는다.
- 하지만 관심 있는 이성이 이미 커플이라면, 그 커플을 깨부순 뒤에 원하던 사랑을 쟁취한다. 다만, 지금 당장 행복한 커플을 내가 강제로 헤어지게 할 수는 없으므로 그 커플 중에서 동성이 새로운 이성과 바람나게 해야 한다.
내가 남자라면, 관심가는 여자를 쟁탈하기 위하여 그녀의 남자친구에게 새로운 여자를 소개시켜주는 것과 같다.
이분 그래프 (Bipartite Graph)
이분 그래프: 어느 그래프 $G$에 속해있는 모든 vertex를 두 그룹 $V_L$과 $V_R$으로 나누었을 때, 그래프 내의 모든 edge $e$의 양 끝이 $v_l \in V_L$ 과 $v_r \in V_R$ 인 그래프를 의미한다. [출처]
따라서, 임의의 $v_{l1}, v_{l2} \in V_L$ 에 대해 $v_{l1}$ 과 $v_{l2}$ 사이에는 edge가 존재하지 않는다. $V_R$ 에 대해서도 마찬가지.
Biphartite Graph Coloring: 그래프 vertex에 $Red$와 $Blue$의 2가지 색으로 칠했을 때, 인접한 vertex가 동일한 색을 갖지 않도록 할 수 있는 그래프를 말한다.


이분 매칭 (Bipartite Matching)
이분 매칭문제는 이 이분 그래프 위에서 edge를 몇 개 골라서 선택하는 데, 그 edge의 양 끝 vertex가 겹치지 않도록 고르는 문제이다.
일반적으로 주어지는 알고리즘 문제에서의 이분 매칭은 최대값을 구해야 한다. 따라서, edge를 최대한 모두 고르되, 선택된 모든 edge의 양 끝 vertex는 겹치지 않아야 한다.
다음과 같은 그래프가 있다고 하자. 초록색 vertex에 해당하는 $V_L$ 내에서는 edge가 존재하지 않고, 파란색도 마찬가지이다.

이분 매칭
다음은 성공적인 이분 매칭을 나타내는 그래프이다. 그리고 가장 오른쪽은 최대 이분 매칭 중에 하나이다.

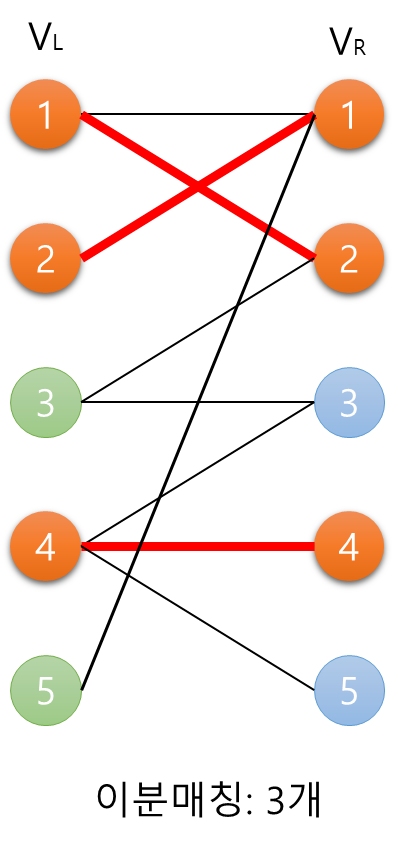

이분 매칭이 아닌 경우

이 경우에는 선택된 두 빨간 edge가 $v_{r1} \in V_R$을 공유하므로 이분매칭이 아니다.
알고리즘 요약
이분 매칭을 찾는 과정으로는 다음과 같다.
1. $V_L$에 속해있는 모든 vertex들을 순차적으로 조사를 시작한다.
2. 현재 조사하고 있는 vertex $v_l \in V_L$와 인접해 있는 모든 $v_r \in V_R$들을 한 번씩 조회해본다. 만약 $v_r$이 기존에 매칭이 없어서 연결할 수 있다면 곧바로 연결하고 $v_l$에 대한 조사를 종료한다.
3. 만약 $v_r$이 다른 노드와 이미 매칭을 맺고 있다면, 현재 $v_r$과 연결되어 있는 또 다른 노드 $v_{l2}$가 다른 매칭 가능 방법이 없는지를 조사한다.
$\rightarrow$ 이 경우에는 $v_{l2}$에 대해서 이분 매칭 조사를 다시 실행해야 하며, $v_r$과는 다른 새로운 $v_{r2} \in V_R$을 찾을 수 있는지 알아내야 한다.
예제
위 그림을 예시로 (boj 11375 예제) 사용
1. $v_{l1}$ 매칭 찾기

$v_{l1} \in V_L$에 대해서 매칭을 시도한다. 인접한 vertex로는 $v_{r1}$과 $v_{r2}$ 존재하므로 이들을 순차적으로 조사한다.
$v_{r1}은 현재 맺고 있는 매칭이 없으므로 이와 바로 매칭을 맺고 종료한다.
2. $v_{l2}$ 매칭 찾기

$v_{l2}$와 인접한 vertex로는 $v_{r1}$ 만 존재한다. $v_{l2}$가 $v_{r1}$와 매칭을 지을 수 있는 가능성이 있는지를 조사한다.

현재 우선 임시로 $v_{l2}$와 $v_{r1}$가 매칭을 맺어 본 상황이다. $v_{l1}$은 새로운 매칭의 가능성이 있는지 다시 조사한다. 단, $v_{r1}$은 후보에서 제외한다.
$v_{l1}$은 이 상황에서 $v_{r2}$가 가능한 것을 알 수 있다.
따라서 $v_{l2}$까지 매칭 된 결과는 다음과 같다.
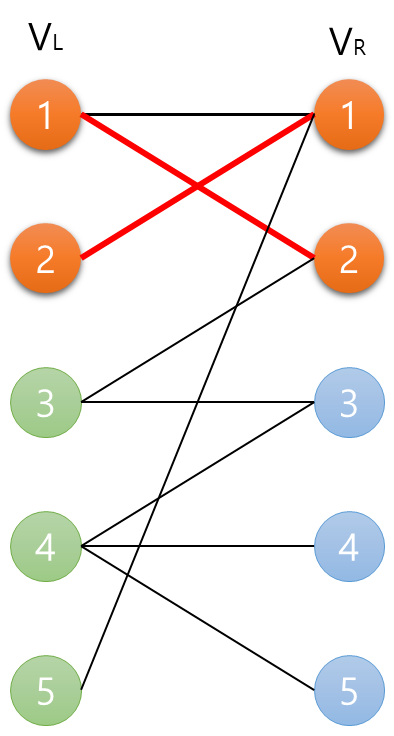
3. $v_{l3}$ 매칭 찾기
$v_{l3}$의 인접 노드로는 $v_{r2}$, $v_{r3}$, $v_{r4}$가 있다. $v_{r2}$와 매칭이 가능한지 확인해보자.

좌측: $v_{l3}$과 $v_{r2}$를 매칭 지었다고 가정하자. 그러면 기존에 $v_{r2}$와 매칭을 맺고 있던 $v_{l1}$가 매칭을 잃게된다.
가운데: 따라서 $v_{l1}$도 가능한 매칭을 찾아보기 위해 자신의 인접 노드들을 차례로 조사한다. 그 중에서 $v_{r1}$을 조사한다.
우측: 만약 $v_{l1}$과 $v_{r1}$이 매칭을 맺는다고 가정하면, $v_{l2}$가 매칭을 잃게 된다. 하지만 $v_{l2}$는 매칭을 맺을 수 있는 방법이 없다. ($v_{r1}$은 $v_{l1}$과 맺어졌다고 가정한 상황이므로)
결론: $v_{l3}$은 $v_{r2}$와 매칭을 맺을 수 없다.
그 다음으로는 $v_{r3}$과 매칭을 맺을 수 있는지 시도한다. $v_{r3}$은 누구와도 매칭을 맺지 않았으므로 바로 매칭을 맺는다.

4. $v_{l4}$ 매칭 찾기
$v_{l4}$의 인접 노드로는 $v_{r3}$, $v_{r4}$, $v_{r5}$가 있다.
$v_{r3}$으로의 매칭 시도는 $v_{l3}$으로 하여금 위에서 겪었던 3번 과정 ( $V_{l3}$의 $V_{r2}$ 매칭 시도 )을 다시 겪게 한다. 하지만 $v_{l3}$은 $v_{r2}$와 맺을 수 없음을 우리는 확인 했다 (우리는 아는 사실이지만 코드상으로는 다시 확인하게 작성하였다).
결국 $v_{l3}$은 $v_{r3}$과 매칭을 시도해야 하는데, $v_{r3}$은 $v_{l4}$가 매칭되어 있다고 가정한 상태이므로 $v_{l3}$은 매칭을 찾을 수 없다.
결론: $v_{l4}$는 $v_{r3}$과 매칭을 맺을 수 없다.
$v_{r4}$는 바로 매칭을 맺을 수 있다.

5. $v_{l5}$ 매칭 찾기
$v_{l5}$의 인접 노드로는 $v_{r1}$가 있다.
$v_{l5}$와 $v_{r1}$을 매칭시킨다고 가정하면, $v_{l2}$에게 새로운 매칭을 제공해야 한다. 하지만 그럴 수 없으므로 실패한다.
결론: $v_{l5}$는 $v_{r1}$과 매칭을 맺을 수 없다.
6. 최종 결과

우리의 알고리즘 최종 결과이다. 최대 이분 매칭의 값은 정해져 있지만, 실제로 선택되는 edge들의 구성은 유일하지 않을 수 있다.
시간복잡도

이분 매칭 알고리즘은 최대 유량 알고리즘과 연관이 깊다. 각 간선의 유량이 1이라고 가정한 상태에서 최대 유량을 흘려 보내는 것이기 때문. DFS로 구하는 과정은 Ford-Fulkerson 알고리즘에 해당하고, Ford-Fulkerson 알고리즘의 시간 복잡도는 $O(EF)$다. 여기서 $F$는 그래프 내에서 흐를 수 있는 최대 유량이고, 이분매칭 알고리즘에서는 많이 흘러도 $min(|V_L|, |V_R|) = O(V)$만큼 흐를 수 있다. 따라서 $O(VE)$.
출처: CLRS 4th edition, 라이님 블로그
이분매칭을 구하는데 더 좋은 시간복잡도가 있는 것으로 보인다: http://en.wikipedia.org/wiki/Hopcroft%E2%80%93Karp_algorithm
코드 (boj 11375)
https://www.acmicpc.net/problem/11375
11375번: 열혈강호
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 한 개의 일만 할 수 있고, 각각
www.acmicpc.net
RUST
- 이번 문제는 입력의 양이 많지 않아서 I/O template 없이 작성
- RUST로 코드를 짜다보면 이 변수가 값이 변할지 변하지 않을지 고민하게 되는 묘한 재미에 빠지게 된다. 변수가 함수에 들어갈 때, (im)mutable이어야 할까?
C++
#include<stdio.h>
#include<vector>
#include<string.h>
using namespace std;
int N, M;
vector<int> graph[1001];
int checked[1001];
char visited[1001];
int dfs(int node){
for(int i=0; i<graph[node].size(); i++){
int next = graph[node][i];
if(visited[next]) return 0;
visited[next] = 1;
if(!checked[next] || dfs(checked[next])){
checked[next] = node;
return 1;
}
}
return 0;
}
int main(){
scanf("%d %d",&N, &M);
for(int i=1; i<=N; i++){
int a;
scanf("%d",&a);
for(int j=0; j<a; j++){
int t;
scanf("%d", &t);
graph[i].push_back(t);
}
}
int Ans = 0;
for(int i=1; i<=N; i++){
memset(visited, 0, 1001);
Ans += dfs(i);
}
printf("%d\n",Ans);
}
RUST
use std::io::{stdin, Read};
fn dfs(i: usize, graph: &Vec<Vec<usize>>, mut parent: &mut[usize;1001], mut visited: &mut[bool;1001]) -> bool{
let graph_iter = graph[i].iter();
for _j in graph_iter{
if visited[*_j]{
continue;
}
visited[*_j] = true;
if parent[*_j] == 0 || dfs(parent[*_j], graph, parent, visited){
parent[*_j] = i;
return true;
}
}
false
}
fn main() {
// 1. Input graph
let mut input = String::new();
stdin().read_to_string(&mut input).unwrap();
let mut input = input.split_ascii_whitespace().flat_map(str::parse::<usize>);
let N = input.next().unwrap();
let M = input.next().unwrap();
let mut graph: Vec<Vec<usize>> = vec![Vec::new(); N+1];
let mut parent: [usize; 1001] = [0; 1001];
for _i in 1..(N+1){
let w = input.next().unwrap();
for _j in 0..w{
let a = input.next().unwrap();
graph[_i].push(a);
}
}
// 2. do DFS sequentially
let mut ANS = 0;
for _i in 1..(N+1){
let mut visited: [bool; 1001] = [false; 1001];
if dfs(_i, &graph, &mut parent, &mut visited){
ANS += 1;
}
}
println!("{ANS}");
}'알고리즘 (Algorihtm) > 공통' 카테고리의 다른 글
| 최소신장트리 (Minimum Spanning Tree) - 크루스칼 알고리즘 (1) | 2023.10.29 |
|---|---|
| 최소신장트리 (Minimum Spanning Tree) - 프림 알고리즘 (0) | 2023.10.29 |
| VScode 설치, 원격 서버 접속 (0) | 2023.10.15 |
| 스위핑 (Sweeping) (0) | 2021.07.20 |
| 세그먼트 트리 (Segment Tree) (0) | 2021.07.02 |




