- Today
- Total
Byeo
boj 16975 - 수열과 쿼리 21 본문
목차
개요
해당 문제는 Segment Tree를 변형하여 사용하는 문제입니다.
이 문제에서 Segment Tree는 기존에 알던 부분 합, 부분 곱, 최소값, 최대값 등을 사용하는 것이 아니라 현재까지 어떤 query들이 어떤 구간에 영향을 주는 지를 저장하기 위해 사용합니다.
즉, 1 a b c 의 query가 들어오면, a ~ b 구간에 c라는 값을 더해야 합니다. 그런데 일일이 a, a+1, a+2, ..., b-1, b 까지 더하는 과정은 시간 소요가 크므로, a ~ b 구간을 담당하는 segment tree node에 일단 저장을 해놓습니다.
다음 2 a 의 query가 들어오면, root node부터 leaf node까지 내려가면서 그 동안 저장되어 있던 segment node의 값들을 전부 더하면 되지요.
설명
boj의 예제로 간단히 살펴보겠습니다.
5
1 2 3 4 5
4
1 3 4 6
2 3
1 1 3 -2
2 3먼저 segment tree 초기는 다음과 같이 구성됩니다.

Step 1 : query 1 3 4 6
이제 1 3 4 6이 다음 입력으로 들어왔을 때를 살펴봅시다.
1 3 4 6은 3번째 ~ 4번째 원소들을 모두 6씩 더하겠다 입니다. 여기서 우리의 배열은 0번부터 시작하므로 이에 맞도록 i = 2 ~ 3 에 더해줘야 합니다.
2 ~ 3의 구간에 6을 더해주는 것은 이제 다음 그림처럼 그릴 수 있습니다.
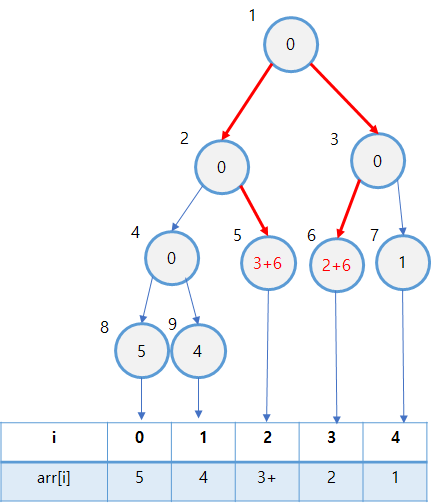
Step 2 : query 2 3
query 2 3은 3 번째 원소의 값을 찾는 질의입니다. 마찬가지로 우리 배열은 0번부터 시작하므로 arr[2]에 해당하는 값을 찾아야 겠네요.
Root node부터 2번을 관리하는 segment tree의 leaf node까지 훑어 내려가면서 나오는 모든 중간 node의 값들을 더해야 합니다. 이 값들은 query 1을 통해서 현재 검색하고자 하는 index에 더하고자 했던 값들이기 때문이죠.

따라서, query 2 3의 경우 0+0+9 = 9가 됩니다.
Step 3 : query 1 1 3 -2
1 1 3 -2 도 마찬가지로 0번 ~ 2번을 관할하는 segment tree node에 -2를 기록해 놓으면 됩니다.
그림에서 2번 node가 0번 ~ 2번의 부분을 관리하므로 여기에 -2를 기록해 놓으면 되겠네요!

Step 4 : query 2 3
Step 2와 동일합니다.
Root node에서 Leaf node까지 훑으면서 나온 모든 값들을 더해주면 됩니다.

여기서 0-2+9 이므로 7이 되겠네요.
코드
※주의할 점
- 입력의 Index 번호와 실제 배열에서의 index를 맞추기 위해 입력받은 범위 값을 -1씩 해줘야 합니다.
#include<stdio.h>
int arr[100000];
class Tree{
long long int node[1<<20];
public:
void Init(int cur, int left, int right){
if(left==right){
node[cur] = arr[left];
return;
}
int mid = (left+right)/2;
Init(cur*2,left,mid);
Init(cur*2+1,mid+1,right);
}
void RangeSum(int cur, int left, int right, int start, int end, int val){
if(start >= left && end <= right){
node[cur] += val;
return;
}
int mid = (start+end)/2;
if(left<=mid) RangeSum(cur*2, left, right, start, mid, val);
if(right>mid) RangeSum(cur*2+1, left, right, mid+1, end, val);
}
long long int Search(int cur, int left, int right, int index){
if(left == right){
return node[cur];
}
int mid = (left+right)/2;
if(index <= mid) return Search(cur*2, left, mid, index) + node[cur];
if(index > mid) return Search(cur*2+1, mid+1, right, index) + node[cur];
}
};
int main(){
int N;
scanf("%d", &N);
for(int i=0; i<N; i++){
scanf("%d",&arr[i]);
}
int M;
scanf("%d",&M);
Tree *t = new Tree();
t->Init(1, 0, N-1);
for(int i=0; i<M; i++){
int q,a,b,c;
scanf("%d",&q);
if(q==1){
scanf("%d %d %d",&a,&b,&c);
a--;b--;
t->RangeSum(1, a, b, 0, N-1, c);
}else{
scanf("%d",&a);
a--;
printf("%lld\n",t->Search(1, 0, N-1, a));
}
}
return 0;
}'알고리즘 (Algorihtm) > 백준' 카테고리의 다른 글
| boj 2836 - 수상 택시 (0) | 2021.07.21 |
|---|---|
| boj 1168 - 요세푸스 문제 2 (2) | 2021.07.15 |
| boj 11659 - 구간 합 구하기 4 (0) | 2021.07.15 |
| boj 12899 - 데이터 구조 (0) | 2021.07.14 |
| boj 9345 - 디지털 비디오 디스크(DVDs) (0) | 2021.07.13 |




