- Today
- Total
Byeo
boj 12899 - 데이터 구조 본문
boj 12899 - 데이터 구조
목차
개요
이 문제는 Binary search 과정과 유사한 문제입니다. 다만, "X보다 작은 수는 몇 개 있는가?" 를 쉽게 알아내기 위하여, 이 과정에서 부분 합 segment tree를 사용합니다.
먼저, 2,000,000개의 배열을 관리할 수 있는 segment tree를 구성합니다.
1번 query 가 들어온 경우 : 요청 값을 a라 했을 때, a를 담당하는 leaf 노드를 찾아 그 값에 +1을 해준 뒤 순차적으로 root node까지 update해나갑니다.
2번 query 가 들어온 경우 : 이는 binary search와 유사합니다. Child node 두 개를 살펴 본 뒤에, 내가 몇 번째 원소를 찾느냐에 따라 왼쪽 혹은 오른쪽 중 하나만 고르면 됩니다. leaf node까지 반복해서 원소를 찾고나면 (항상 존재함은 문제에 의해 보장됨) delete까지 같이 해주면 됩니다.
설명
다음과 같은 예제를 수행한다고 해보죠
8
1 1
1 5
1 7
1 8
1 10
2 1
2 2
2 31번 Query
1번 query는 금방 파악하셨으리라 생각합니다.
먼저 처음에 다음과 같이 segment tree를 초기화 시켜줍니다.
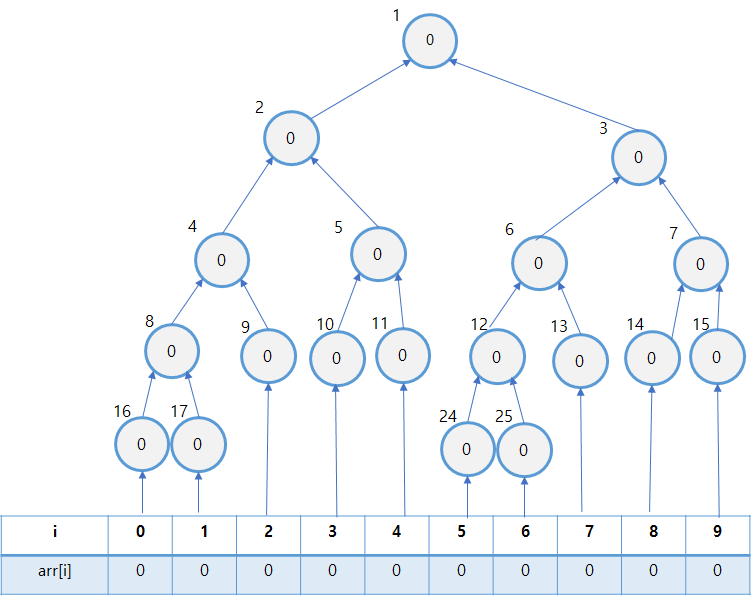
이 포스트에서는 편의상 수 입력이 1 ~ 10 사이에서만 들어온다고 가정하겠습니다. boj 12899의 경우, 앞서 설명된 것 처럼 입력 가능한 수의 범위인 2,000,000개의 배열을 미리 잡아 놓아야 합니다.
1 1
1 5
1 7
1 8
1 10다음 이 1번 query들을 수행하는 과정은, arr[a-1]에 값을 1 더해주고 부분 합 tree를 갱신한 것과 같습니다.
※ 1을 더해줘야 몇 개가 중복되어 있는지 알 수 있습니다. 단순히 1을 대입하면, 같은 수가 1번 query로 들어왔을 때 처리할 수 없습니다.
그 결과 아래와 같이 segment tree가 구성 될 것입니다!

Query 2번
이제 어떻게 찾고, 지울지에 대해서 알아봅시다!
2 1
2 2
2 3Step 1 : query 2 1
먼저 가장 작은 수 (2 1) 를 찾고 지워봅시다.
Root node부터 시작해서 1st 위치가 어디 있는지를 파악해야 합니다. 이를 위해서 left child의 부분 합과 비교해보면 됩니다. 배열은 오름차순으로 관리되고 있기 때문에, left child가 관리하는 모든 수는 right child가 관리하는 모든 수보다 작음이 보장됩니다.
우리가 찾고자 하는 k th를 rank라 해보죠.
Root node에서 rank (1)는 left child의 값 (2) 이하이므로 left child를 선택하면 됩니다.

이런 방법으로 계속 찾아나가면 0번 index가 선택 될 것입니다. 따라서 index 번호를 return 해주면 되겠죠! (출력할 때는 이 return 값에 1을 더해서 출력해야 합니다.)

이제 문제에서 삭제도 요구하므로 배열의 0번과 관련된 node들의 value를 하나씩 감소 시키면서 parent를 update 해나가면 됩니다.
마찬가지로 중복 처리를 위해 0을 대입하는 것이 아니라 1을 감소 시켜야 합니다.

Step 2 : query 2 2
마찬가지로 2nd 작은 원소를 지우기 위해서는 root node부터 left child와 값을 비교해야 합니다. 그런데, left child의 값 1은 rank 값 2보다 작으므로, 우리가 찾고자 하는 원소는 오른쪽 subtree에 있음을 알 수 있습니다.

이제 여기서 주의해야 할 점이 있습니다.
우리가 찾고자 하는 값은 이제 right child에서 k th 의 원소가 아니라 k - node[left_child] th 를 찾아야 합니다.
즉, root node에서 왼쪽에 1개, 오른쪽에 3개가 있는 상황입니다. 2nd 원소를 찾기 위해서는 오른쪽을 살펴 봐야 하는데, 이미 왼쪽에 1개의 작은 원소가 있었죠. 따라서 오른쪽에서 2nd 작은 원소가 아닌 1st 작은 원소를 찾아야 합니다.
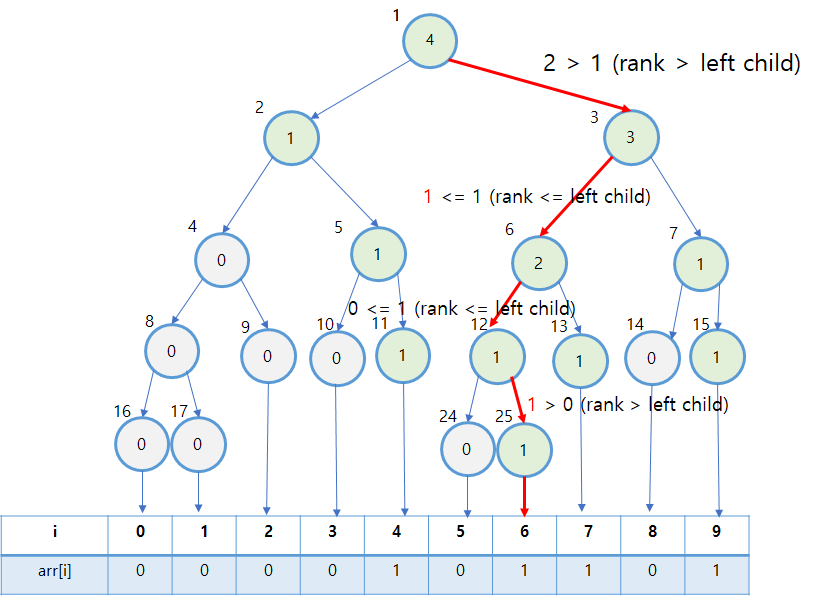
현재 찾은 값은 6번 노드네요. 이제 6을 return해주고 값을 감소 시킨 뒤 parent들을 순차적으로 update 해나가면 됩니다.

Step 3 : query 2 3
마찬가지로 수행하면 됩니다.

코드
- 먼저 2,000,000개의 leaf node들을 관리할 수 있는 segment tree를 구성해야 합니다.
공식 $2^{\lceil{log_2 {N}}\rceil +1} = 2^{\lceil{log_2 {2,000,000}}\rceil +1} <= 2^{22}$ 이므로[세그먼트 트리(Segment Tree)] 1<<22 만큼 segment tree를 생성하였습니다.
※주의할 점
- index에 유의해야 합니다. Input의 범위는 1 ~ 2,000,000인데 반해 우리가 관리하고자 하는 배열의 index는 0 ~
1,999,999입니다. - K th 값을 찾는 과정은 binary search와 유사합니다. 다만, right subtree를 찾을 때는 K 값을 left child의 값 만큼 빼줘야 합니다.
#include<stdio.h>
#define IMAX 2000000
using namespace std;
class Tree{
int node[1<<22];
public:
int Insert(int cur, int left, int right, int index){
if(left==right){
node[cur] += 1;
return node[cur];
}
int mid = (left+right)/2;
int ret = 0;
if(index <= mid) Insert(cur*2, left, mid, index);
if(index > mid) Insert(cur*2+1, mid+1, right, index);
return node[cur]= node[cur*2] + node[cur*2+1];
}
int Delete(int cur, int left, int right, int rank){
if(left==right){
node[cur] -= 1;
return left;
}
int mid = (left+right)/2;
int ret = 0;
if(rank <= node[cur*2]) ret = Delete(cur*2, left, mid, rank);
//right subtree를 볼 때는 query의 rank를 바꿔줘야함 (node[left_child]의 값 만큼 제해야함)
else ret = Delete(cur*2+1, mid+1, right, rank-node[cur*2]);
node[cur] = node[cur*2] + node[cur*2+1];
return ret;
}
};
int main(){
int N;
scanf("%d",&N);
Tree *t = new Tree();
for(int i=0;i<N;i++){
int q,a;
scanf("%d %d",&q,&a);
if(q==1){
t->Insert(1, 0, IMAX-1, a-1);
}else{
printf("%d\n",t->Delete(1,0,IMAX-1,a)+1);
}
}
}'알고리즘 (Algorihtm) > 백준' 카테고리의 다른 글
| boj 16975 - 수열과 쿼리 21 (0) | 2021.07.15 |
|---|---|
| boj 11659 - 구간 합 구하기 4 (0) | 2021.07.15 |
| boj 9345 - 디지털 비디오 디스크(DVDs) (0) | 2021.07.13 |
| boj 2357 - 최솟값과 최댓값 (0) | 2021.07.12 |
| boj 11505 - 구간 곱 구하기 (1) | 2021.07.02 |




