- Today
- Total
Byeo
boj 1017 - 소수쌍 본문
개요
이분매칭 알고리즘의 응용버전입니다. 모든 수끼리 매칭을 시켰을 때, 모든 수의 쌍의 합이 소수가 될 수 있는 경우를 알아내는 문제죠.
핵심은 다음과 같이 3가지로 볼 수 있습니다.
1. 소수 판별 알고리즘은 에라토스테네스의 체로 구현한다. (설명은 위키로 대체: 위키 링크)
2. 모든 수가 매칭을 이뤄야 하므로 이분 매칭 알고리즘에서 매칭의 개수가 $n/2$ 인 케이스를 찾아내면 된다.
3. 2를 제외한 소수는 모두 홀수이다. 따라서 좌측 노드는 짝수, 우측 노드는 홀수로 나누어서 매칭을 실행하면 된다. (중복되는 수가 주어지지 않으므로 1 + 1 과 같은 케이스는 없다.)
예제
백준 예제 입력 1번을 살펴보겠습니다.
6
1 4 7 10 11 12
1. 소수 배열 만들기
가장 먼저 에라토스테네스의 체 알고리즘을 이용해서 소수들을 구합니다. 1,000 이하의 숫자가 들어오므로 최대 2,000까지만 구하면 됩니다.
이 예제에서는 가능한 가장 큰 합이 23이므로 23까지만 표기하겠습니다.

2. 이분매칭 그래프 구성
Vertex 나누기
2를 제외한 모든 소수는 홀수입니다. 따라서 우리가 이분매칭 그래프를 생성할 때, 좌측은 모두 홀수 / 우측은 모두 수인 그래프로 구성을 해볼 수 있습니다. (좌측이 짝수, 우측이 홀수여도 상관은 없습니다. 구현의 차이)

여기서!! $|V_L| != |V_R|$ 이면 더이상 알고리즘을 진행할 필요도 없이 -1을 뱉으면 됩니다! (이유는 생각해보기)
Vextex 연결
이제 $V_L$과 $V_R$에 몇 개의 edge를 연결하여 이분매칭 그래프를 완성해줍니다. 여기서 edge를 긋는 조건은 두 vertex를 연결했을 때 합이 소수인 경우만 그어줍니다.
$|V_L| \times |V_R|$의 경우의 수를 모두 판단해야 하긴 합니다. 이 때 위에서 에라토스테네스의 체로 구해놓았던 배열을 이용하면 빠르게 판별이 가능하겠죠?

$1+4 = 5, isprime[5] = true$ 이므로 소수라서 연결, ...
$11+4 = 15, isprime[15] = false$ 이므로 소수가 아니라서 연결하지 않음, ...
3. 이분매칭 알고리즘 실행
이분매칭 알고리즘을 실행합니다. 문제 조건에 따라 매칭의 수가 $n/2$ (이 예제에서는 3)이 되는 경우를 찾아야 합니다.
단, 첫 번째 숫자를 기준으로 모든 경우의 수를 찾아야 하므로 첫 번째 숫자는 우선 하나를 매칭시켜놓고 시작합니다.
1과 4를 매칭

왼쪽과 같이 1을 4와 매칭시켜 놓고나면, 오른쪽과 같이 나머지 vertex들도 전부 이분매칭이 가능합니다. 따라서 4는 정답리스트에 포함됩니다.
1과 10를 매칭
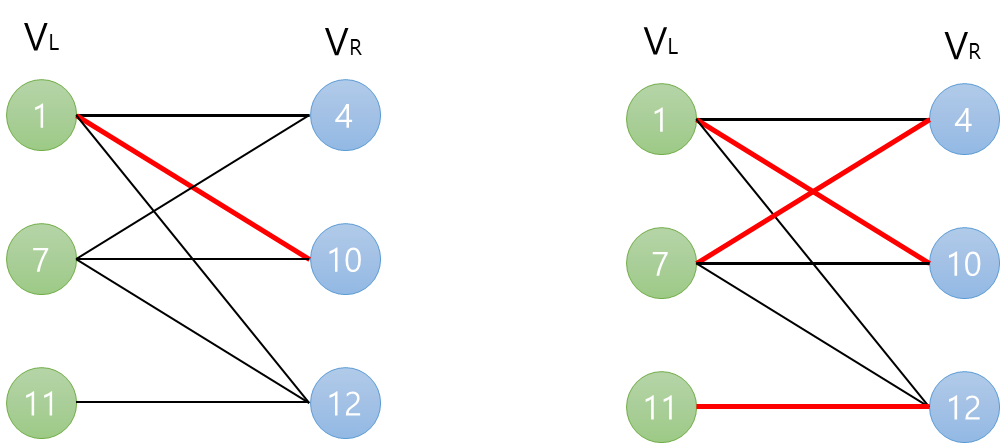
1과 10을 매칭시킨 경우에도 오른쪽과 같이 가능하네요. 따라서 10도 정답 리스트에 포함됩니다.
1과 12를 매칭
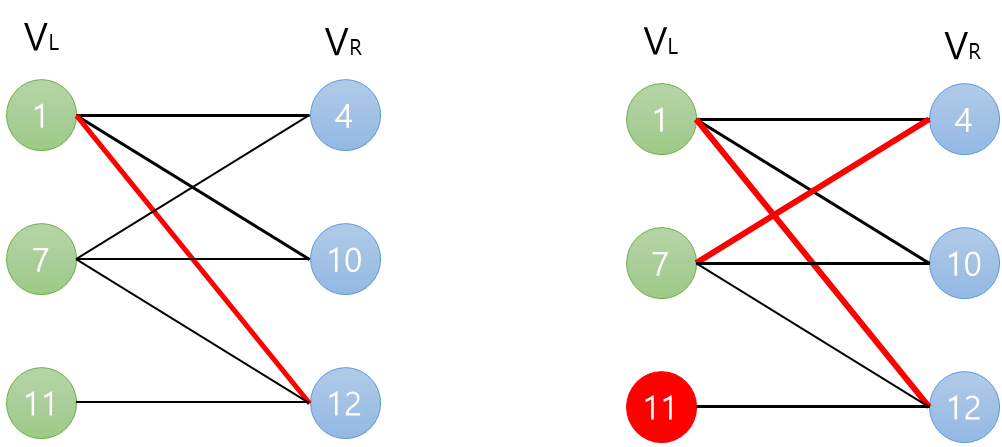
1과 12를 매칭한 경우에는 11의 짝을 찾을 수 없습니다. 따라서 불가능합니다.
정답
결국 정답은
4 10이 됩니다.
코드
Rust로 짜긴 했는데... 다시 C++로 회귀할 예정입니다!
use std::io::{stdin, Read};
const PARENT_DEFAULT: usize = 99;
fn eratosthenes(prime: &mut [bool; 2001]) -> (){
prime[1] = false;
prime[2] = true;
for i in 2..2001 {
if prime[i] {
let mut j = i * 2;
while j < 2001{
prime[j] = false;
j += i;
}
}
}
}
fn dfs(i: usize, graph: &Vec<Vec<usize>>, parent: &mut [usize; 26], visited: &mut [bool; 26]) -> usize{
for next in graph[i].iter(){
if visited[*next]{
continue;
}
visited[*next] = true;
if parent[*next] == PARENT_DEFAULT || dfs(parent[*next], graph, parent, visited) == 1{
parent[*next] = i;
return 1;
}
}
0
}
fn main() {
// 1. Get Inputs from stdin
let mut input = String::new();
stdin().read_to_string(&mut input).unwrap();
let mut input = input.split_ascii_whitespace().flat_map(str::parse::<usize>);
let N = input.next().unwrap();
let mut flag : usize = 0;
let mut numbers: [[usize; 50]; 2] = [[0; 50]; 2];
let mut flag_cnt: usize = 0;
let mut flag_xor_cnt: usize = 0;
for _n in 0..N {
let input_num = input.next().unwrap();
if _n == 0{
flag = input_num % 2;
}
numbers[input_num % 2][if input_num % 2 == flag {flag_cnt} else {flag_xor_cnt}] = input_num;
if input_num % 2 == flag {flag_cnt += 1} else {flag_xor_cnt += 1};
}
// 1-1. shortcut
if flag_cnt != flag_xor_cnt {
println!("-1");
return;
}
// 2. Do Sieve of Eratosthenes
let mut prime: [bool; 2001] = [true; 2001];
eratosthenes(&mut prime);
// 3. Create Graph
let mut graph: Vec<Vec<usize>> = vec![Vec::new(); N/2];
for _i in 0..flag_cnt{
for _j in 0..flag_xor_cnt{
if prime[numbers[flag][_i] + numbers[flag^1][_j]] {
graph[_i].push(_j);
}
}
}
// 4. Do Bipartite matching
let mut ANS: Vec<usize> = Vec::new();
for _i in graph[0].iter() {
let mut parent: [usize; 26] = [PARENT_DEFAULT; 26];
parent[*_i] = 0;
let mut result: usize = 1;
for _j in 1..flag_xor_cnt{
let mut visited: [bool; 26] = [false; 26];
visited[*_i] = true;
result += dfs(_j, &graph, &mut parent, &mut visited);
}
if result == N/2 {
ANS.push(numbers[flag^1][*_i]);
}
}
//5. Sorting
if ANS.len() == 0 {
print!("-1");
return;
}
ANS.sort();
for _a in ANS.iter(){
print!("{} ", *_a);
}
}'알고리즘 (Algorihtm) > 백준' 카테고리의 다른 글
| boj 1671 - 상어의 저녁식사 (0) | 2024.03.02 |
|---|---|
| boj 1867 - 돌맹이 제거 (0) | 2024.03.02 |
| boj 11376 - 열혈강호 2 (0) | 2024.01.14 |
| boj 11014 - 컨닝 2 (0) | 2024.01.11 |
| boj 17435 - 합성함수와 쿼리 (0) | 2023.12.25 |



